In my previous post RC Circuit Analysis , I have described the fundamentals of simple Analog RC circuit which is the backbone of all other RC circuit combination analysis. I highly recommend to go through the previous post RC Circuit Analysis to get familiarize with fundamentals of RC analysis.
In this post we are going discuss the behavior of 1R-2C RC circuit excited with step voltage input. In our analysis all the components are considered ideal.
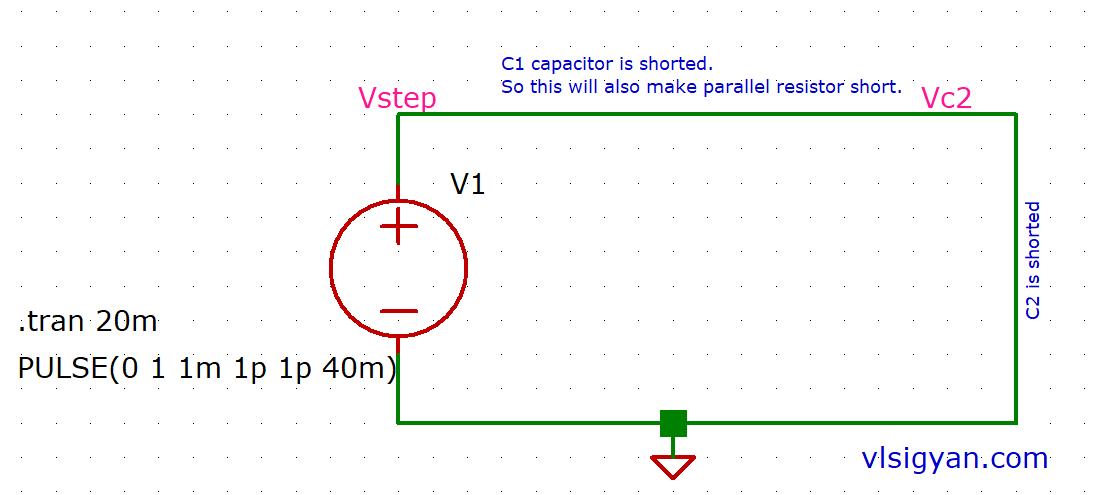
The 1R-2C combination RC circuit is given below.
From our earlier analysis in RC Circuit Analysis , we are aware that we need to find out the voltage across capacitor and current through it at time t=0+ and t=infinity.
Analysis at time t=0+
Now, for the above circuit, before application of voltage inputs capacitors are fully discharged (voltage across them= 0 v). After application of step voltage, from the fundamental property of capacitors, the capacitor will prevent the sudden change of the voltage across it and will try to remain at voltage=0. But, for the above circuit, considering all the elements are ideal, a unique incident takes place.
From our previous analysis, at ![]() the circuit will look like below.
the circuit will look like below.
The above circuit at t=0+ violates Kirchoff’s voltage law (KVL).
![]() >
> ![]() , but we know
, but we know ![]() is not zero at
is not zero at ![]() .
.
To satisfy KVL, the voltage across capacitor (capacitor charge ![]() ) gets distributed at
) gets distributed at ![]() and capacitor voltages changes abruptly at
and capacitor voltages changes abruptly at ![]() ( all ideal capacitors). Now, to change voltage across capacitor we need infinite amount of current or in a word we need impulse current. From the fundamental i-v equation of capacitor, capacitor integrates current to get the voltage. So when impulse current gets integrated we get step voltage which changes the voltage across capacitor abruptly at
( all ideal capacitors). Now, to change voltage across capacitor we need infinite amount of current or in a word we need impulse current. From the fundamental i-v equation of capacitor, capacitor integrates current to get the voltage. So when impulse current gets integrated we get step voltage which changes the voltage across capacitor abruptly at ![]() . This gives us the voltage across capacitor at
. This gives us the voltage across capacitor at ![]() . Below is the circuit, at
. Below is the circuit, at ![]()
From the voltage divider formula of capacitors in series, we can write
Voltage across capacitor C1,
![]()
Voltage across capacitor C2,
![]()
Analysis at time t=infinity
From our previous post with 1R-1C circuit, we know that when capacitor is fully charged it acts like an open circuit and no current flows through it. As in this circuit two capacitors are there we need to find out the what would be the voltage at at t=infinity. We need to keep in mind that KCL and KVL should satisfy at each point of our analysis of RC circuits.
Keeping this in mind, at t=infinity, let’s say capacitor ![]() charges fully, behaves as an open circuit and current flowing through is zero. As this is a series circuit, the current through
charges fully, behaves as an open circuit and current flowing through is zero. As this is a series circuit, the current through ![]() is same as the current through the input voltage source
is same as the current through the input voltage source ![]() and parallel combination of
and parallel combination of ![]() .
.
So, when current through a resistor is zero the voltage across it is also zero. This gives us the voltage across C1 at t=infinity,
![]()
Voltage across C2 at t=infinity, using KVL,
![]()
The time constant of circuit can be calculated by shorting the voltage source and calculating ![]() and
and ![]() .
.
Here, ![]()
Below shows the simulation result in LTspice.
Feel free to comment if you have any questions/suggestions.